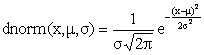integrate(f,var,a,b)

The integrate function returns an approximation for the numerical integral of f with the variable var from a to b. This is mathematically written as:

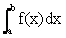
This integral is the same as the area between the function f and the x-axis from a to b where the area under the axis is counted negative. f may be any function with the variable indicated as the second argument var. a and b may be any numeric expressions that evaluate to real numbers or they can be -INF or INF to indicate negative or positive infinity. integrate does not calculate the integral exactly. Instead the calculation is done using the Gauss-Kronrod 21-point integration rule adaptively to an estimated relative error less than 10^-3.

f(x)=integrate(t^2-7t+1, t, -3, 15) will integrate f(t)=t^2-7t+1 from -3 to 15 and evaluate to 396. More useful is f(x)=integrate(s*sin(s), s, 0, x). This will plot the definite integral of f(s)=s*sin(s) from 0 to x, which is the same as the indefinite integral of f(x)=x*sin(x).

sum(f,var,a,b)

The sum function returns the summation of f where var is evaluated for all integers from a to b. This is mathematically written as:

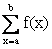
f may be any function with the variable indicated as the second argument var. a and b may be any numeric expressions that evaluate to integers.

product(f,var,a,b)

The product function returns the product of f where var is evaluated for all integers from a to b. This is mathematically written as:

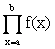
f may be any function with the variable indicated as the second argument var. a and b may be any numeric expressions that evaluate to integers.

fact(n)

The fact function returns the factorial of n, commonly written as n!. n may be any numeric expression that evaluates to a positive integer. The function is defined as fact(n)=n(n-1)(n-2)...1, and relates to the gamma function as fact(n)=gamma(n+1).

gamma(z)

The gamma function returns the result of the Euler gamma function of z, commonly written as Γ(z). z may be any numeric expression that evaluates to a real number or a complex number. The gamma function relates to the factorial function as fact(n)=gamma(n+1). The mathematical definition of the gamma function is:

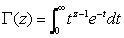
This cannot be calculated precisely, so Graph is using the Lanczos approximation to calculate the gamma function.

beta(m, n)

The beta function returns the result of the Euler beta function evaluated for m and n. m and n may be any numeric expressions that evaluate to real numbers or complex numbers. The beta function relates to the gamma function as beta(m, n) = gamma(m) * gamma(n) / gamma(m+n).

W(z)

The W function returns the result of the Lambert W-function, also known as the omega function, evaluated for z. z may be any numeric expression that evaluates to a real number or a complex number. The inverse of the W function is given by f(W)=W*e^W.

For real values of z when z < -1/e, the W function will evaluate to values with an imaginary part.

zeta(z)

The zeta function returns the result of the Riemann Zeta function, commonly written as ζ(s). z may be any numeric expression that evaluates to a real number or a complex number.

The zeta function is defined for the whole complex plane except for the pole at z=1.

mod(m,n)

Calculates m modulo n, the remainder of m/n. mod calculates the remainder f, where m = a*n + f for some integer a. The sign of f is always the same as the sign of n. When n=0, mod returns 0. m and n may be any numeric expressions that evaluate to real numbers.

dnorm(x, [μ,σ])

The dnorm function is the probability density of the normal distribution, also called Gaussian distribution. x is the variate, also known as the random variable, μ is the mean value and σ is the standard deviation. μ and σ are optional and if left out the standard normal distribution is used where μ=0 and σ=1. x, μ and σ may be any numeric expressions that evaluate to real numbers where σ > 0. The normal distribution is defined as: