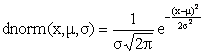integrate(f,var,a,b)

The integrate function returns an approximation for the numerical integral of f with the variable var from a to b. This is mathematically written as:

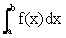
This integral is the same as the area between the function f and the x-axis from a to b where the area under the axis is counted negative. f may be any function with the variable indicated as the second argument var. a and b may be any numerički izrazi that evaluate to realni brojevi or they can be -INF or INF to indicate negative or positive infinity. integrate does not calculate the integral exactly. Instead the calculation is done using the Gauss-Kronrod 21-point integration rule adaptively to an estimated relative error less than 10^-3.

f(x)=integrate(t^2-7t+1, t, -3, 15) will integrate f(t)=t^2-7t+1 from -3 to 15 and evaluate to 396. More useful is f(x)=integrate(s*sin(s), s, 0, x). This will plot the integral of f(s)=s*sin(s) from 0 to x, which is the same as the definite integral of f(x)=x*sin(x).

sum(f,var,a,b)

The sum function returns the summation of f where var is evaluated for all integers from a to b. This is mathematically written as:

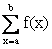
f may be any function with the variable indicated as the second argument var. a and b may be any numerički izrazi that evaluate to integers.

product(f,var,a,b)

The product function returns the product of f where var is evaluated for all integers from a to b. This is mathematically written as:

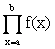
f may be any function with the variable indicated as the second argument var. a and b may be any numerički izrazi that evaluate to integers.

fact(n)

Funkcija fact daje faktorijele od n, najčešće pisano kao n!. n može biti bilo koji numerički izraz koji daje positivni cijeli broj. Funkcija se definira kao fact(n)=n(n-1)(n-2)...1, a gamma funkcija kao fact(n)=gamma(n+1).

gamma(z)

The gamma function returns the result of the Euler gamma function of z, commonly written as Γ(z). z may be any numerički izraz that evaluates to a realni broj or a kompleksni broj. The gamma function relates to the factorial function as fact(n)=gamma(n+1). The mathematical definition of the gamma function is:

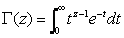
This cannot be calculated precisely, so Graph is using the Lanczos approximation to calculate the gamma function.

beta(m, n)

Funkcija beta daje vrijednost Eulerove beta funkcije argumenta u rasponu od m do n. m i n mogu biti bilo koji numerički izrazi koji su realni brojevi ili kompleksni brojevi. beta funkcija se odnosi prema gamma funkciji kao beta(m, n) = gamma(m) * gamma(n) / gamma(m+n).

W(z)

Funkcija W poznata kao omega funkcija, daje vrijednost Lambert W-funkcije za argument z. z može biti bilo koji numerički izraz koji daje realni broj ili kompleksni broj. Inverzija W funkcije je: f(W)=W*e^W.

Za realne vrijednosti z kad je z < -1/e, W funkcija će sadržavati imaginarni dio.

zeta(z)

Funkcija zeta, najčešće pisana kao ζ(s), daje vrijednost Riemann Zeta funkcije argumenta. z može biti bilo koji numerički izraz koji daje realni broj ili kompleksni broj.

Funkcija zeta je određena u cijeloj kompleksnoj ravnini osim u njenu ishodištuz = 1.

mod(m,n)

Izračunava m modul n i ostatak od m/n. mod izračunava ostatak f, pri čemu je m = a*n + f za cijeli broj a. sign f je isto što i sign od n. Kad je n=0, mod daje 0. m i n mogu biti bilo koji numerički izrazi koji su realni brojevi.

dnorm(x, [μ,σ])

Funkcija dnorm daje vjerojatnost normalne razdiobe, poznate kao Gaussova razdioba. x je promijenjiva, često zvana slučajna varijabla, μ je srednja vrijednost, a σ, standardna devijacija. μ i σ su neobavezne i ako izlaze iz standardne normalne distribucij,e uzima se μ=0 i σ=1. x, μ i σ mogu biti bilo koji numerički izrazi koji su realni brojevi gdje je σ > 0. Normalna distribucija je definirana ovako: